|
因子溢价与因子择时—跨越世纪的实证结果(一)导读 1、作为西学东渐–海外文献推荐系列报告第三十三篇,本文推荐了ANTTI ILMANEN, RONEN ISRAEL等人于2019年发表的论文《Factor Premia and Factor Timing: A Century of Evidence》。 2、文章利用近一个世纪的样本数据深入研究了价值(Value),动量(Momentum),利差(Carry)和防御(Defensive)这四类重要因子在六类资产中的预测效率、收益来源以及预测能力时变性等问题。同时鉴于篇幅原因,我们将文章分为两部分,本文为第一部分,主要包括对因子的预测效率、收益来源的研究 (全部研究成果参见相关研报、第二部分微信稿将于周六推出) 。 3、首先本文将全样本划分为预样本、原始样本期与样本后三个子样本,并通过对比三个子样本因子的表现来探究因子的预测效率。我们发现四类因子在六类资产中:1)样本内表现大多优于样本外,但样本外也存在超额收益。即因子在原始样本中确实存在过拟合但并非所有的因子溢价都源于过拟合;2)预样本和样本后表现差异大多不显著,即我们并未找到套利行为会影响因子溢价的证据。 4、本文从投资者行为和宏观经济风险两方面探究了因子收益来源,结果显示:1)套利行为并没能对因子相关性产生较大影响,这也进一步说明了套利行为对因子溢价几乎没有影响;2)总体而言,几乎没有证据表明这些因子与宏观经济变量(如市场流动性、商业周期等)有显著相关关系。同时因子在不同经济环境下相关性并没有很大变化,特别在极端的负面事件中也没有发现因子之间的相关性上升。 风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成, 在政策、市场环境发生变化时模型存在失效的风险。 一、引言 实证研究表明许多因子能够对横截面收益率进行预测,但对于这些因子的预测效率、收益来源以及预测能力时变性的争论却一直不绝于耳。为了解决这些问题,本文利用长达一个世纪的数据样本,仔细探究了资产定价文献中出现过的四类非常重要的因子在六大类资产中的表现: 1)我们在大量的样本外数据中证明了上述因子溢价的确存在; 2)从风险和行为模型两方面分析这些因子溢价的来源; 3)探究了因子溢价的时变性,以及是否可以对这种时变性进行有效预测。 本文选用了近一个世纪的样本数据来进行测试,如此丰富的样本集为我们的测试带来了一些优势:首先,我们为数据挖掘(过拟合)偏差是否会夸大因子溢价提供了更有说服力的检验,同时也探究了套利行为是否改变了对因子收益的预期;其次,我们的样本集囊括了更多经济冲击事件,例如宏观经济、市场流动性、投资者情绪和崩盘等事件,我们可以测试这些事件对于因子溢价的影响。第三,更长的样本数据为条件因子溢价的研究提供了更为有利的环境,相应的测算结果为不同市场、不同时段资产价格的动态表现提供了新的证据。 本文选用的四类因子适用于多种资产,常被用于资产定价模型中,分别为:价值因子(Value),动量因子(Momentum),利差因子(Carry)和防御因子(Defensive)。实际上针对美国股票市场,目前的学术研究中已经发现了数百个因子,但很多都由于测试所使用的统计方法过于粗糙或缺乏样本外的稳健表现而遭到质疑。我们研究的四类因子在众多市场与资产类别中的样本内外都表现优异,这也是这四类因子至今仍是资产定价研究重点的主要原因。然而即便只关注这四类因子,有关它们预测效率、收益背后的经济逻辑以及表现时变性的争论也一直存在。因此在本文中,我们除了进一步提供关于上述争论的样本外实证结果之外,还从资产定价理论的视角检验了有关因子溢价的不同定价理论: - 过拟合:我们测试了两种类型的过拟合。第一种,是因子溢价全都源于数据挖掘,实际上因子并不能带来超额收益,因此因子溢价会在未测试的时间段或资产类别中消失。第二种是因子溢价确实存在,但会在样本内的测试中被夸大。
- 行为金融学与有限套利:如果因子的超额收益是由于投资者行为偏差产生的,那么需要注意的是这些因子溢价可能会由于投资者套利行为而慢慢消失。一个直观的例子是当因子公开之后,更多的套利资本会追逐这些因子,从而导致因子溢价慢慢减弱。同时这也有可能导致不同因子和不同资产类别的市场表现的相关性更高。综上,因子溢价和相关性可能随着投资者情绪和套利成本的代理变量(如波动性和流动性风险)而变化。
- 理性风险理论:这里包含一系列不同的模型。
a)非条件风险溢价模型。这类模型意味因子可以提供关于非条件随机贴现因子(SDF)的信息。在这种情况下,因子样本内外表现没有显著差异,并且收益相关性结构较稳定,预测能力不随时间变化。 b)时变风险溢价模型。这类模型意味着因子能够提供条件随机贴现因子的有用信息。模型假设风险溢价或因子的风险本身具有明显的时变特征,因子收益的时间序列很可能是可预测性的,且更容易被基于价格的一些指标所发现。 c)特定非条件和条件模型。一些学者提出因子溢价可能与特定的风险有关,例如宏观经济下行、灾害风险等。某些情况下,我们可以找到这些特定风险的合理代理变量,并利用更丰富的样本来测试模型。除了研究这些因子在不同类型的资产中的表现,我们还研究这些市场是否会随时间进行整合以及单一的资产定价框架是否适用于各个市场。 我们首先对价值、动量、利差和防御四类因子溢价的存在性进行确认,并测算了这四类因子在六类资产中的溢价的水平。具体步骤如下:将每个因子的样本划分为三个期间:预样本(因子被发现有效之前)、原始样本期以及样本后的时间区间,然后进行测试。我们的分析方法与Mclean和Pontiff(2016)的类似,但加入了一个特殊的补充-预样本期的测试,预样本是在因子的原始样本期之前的时间期。我们认为在预样本时期套利活动几乎不会发生。通过比较预样本和样本后两个时期的表现,我们可以得到知情交易(套利行为)对因子溢价的影响,同时通过比较样本内(原始样本期),样本外(非原始样本期)的表现来捕捉数据挖掘(过拟合)的影响。 与Mclean和Pontiff(2016)测试结果类似,我们发现这些因子在样本外的表现仅为样本内表现的三分之一。值得注意的是,我们发现四类因子在原始资产类别(因子最先被发现的资产类别)与其他资产类别的收益没有显著差异。综上,我们认为因子存在一定程度的过拟合,即在样本内表现更好,但没有对原始资产类型过拟合,这意味着因子并非仅仅只在原始资产类型上表现好。同时我们对比了预样本和样本后时期的表现,没有发现套利行为会降低因子表现的证据。 我们还发现样本中各因子的表现在资产类别之间略有正相关,与最近的研究结果一致(Asness,Moskowitz,Pedersen(2013),Koijen,Moskowitz,Pedersen,Vrugt(2018),以及Brooks和Moskowitz(2018))。这些相关性随着时间的推移不会改变,进一步证明套利行为并未影响这些因子,并且也表明这些市场在样本初期也并未完全分割。过去一百年中,不同类别的资产中都存在着类似的因子溢价,这一事实对一些资产定价模型形成了挑战。 更丰富的样本也为我们研究经济活动变量对因子溢价的影响奠定了基础。我们测试了因子溢价与经济增长、边缘政治风险、波动风险、尾部风险、市场流动性等变量的关系。我们额外近50年的样本有助于识别低频经济事件的影响,同时多样化的资产类别也有助于降低针对特定资产研究所带来的噪音。然而,尽管有这些优势,我们依然未能证明资产定价因子对经济活动存在着显著的风险敞口。我们所研究的多空因子溢价,相较于资产本身的风险溢价来说,对宏观经济条件的变动更不敏感。 最后,我们试图利用数据更好地捕捉因子的条件风险溢价。众所周知,时变的风险溢价是很难估计的,关于它们存在许多争论,包括对因子择时有效性的怀疑。我们使用更丰富的样本试图捕捉因子的条件风险溢价。虽然因子的条件风险溢价并不能保证因子溢价的可预测性,但由于因子溢价的时间序列可预测性意味着条件收益溢价的存在,我们最终决定使用各种各样的因子择时信号(条件信息)和方法来研究条件风险溢价的存在。同时所有资产类别都存在相同的无条件因子溢价,我们可以测试针对相同因子的择时策略是否在其他资产类别中依旧有效。目前关于因子择时的研究集中于美国股市的因子,我们的数据有助于对因子择时进行样本外的测试。 本文研究了4类因子在6种资产类别中采用的19种方法和11种择时信号所构建的上千种不同择时策略的表现。这些择时策略的收益率使得我们可以将所有的择时模型放在同一个水平上进行量化比较,同时我们也可以对因子择时所带来的相对于静态模型的投资表现的边际改善进行评价。 我们在已实现的因子溢价中发现了显著的时变性,但因子择时策略的效果普遍较弱且反映的结果并不一致。因子择时结果最好的是基于估值差和反向波动率开发的策略,这和其他文献中的研究保持了一致(Asness, Friedman, Krail, and Liew (2000), Cohen, Polk, and Vuolteenaho (2003), and Moreira and Muir (2017))。我们进一步发现,从理论上对时序模型施加经济含义限制(例如Campbell和Thompson(2007)做法)提高了样本外的可预测性。但这个结果在不同因子、不同资产类别上的表现并不一致,这导致人们质疑其稳健性。关于因子动量择时,以及基于其他宏观变量和市场波动所开发的因子择时策略,我们找到的实证支持就更弱了。我们的研究进一步表明,纯粹的实时因子择时策略的表现并不尽如人意,这可能源自于该策略对某些潜在静态因子的暴露,以及更高的换手率和交易成本对收益的侵蚀。 本文通过六个不同资产类别的近一个世纪数据的实证分析,证明了在样本外存在稳定的、共同的因子溢价,同时发现宏观经济对因子溢价的影响有限,因子溢价的时变特征使得我们很难在投资实践中对其进行动态把握。后文内容的具体结构如下: 第二节是本文使用的数据和因子构建方法介绍; 第三节用更丰富的样本测试了因子溢价的存在,并基于测试结果研究数据挖掘(过拟合)和套利行为对因子溢价的影响; 第四节从相关理论出发,测试了因子溢价的种种潜在来源; 第五节给出本文结论。 二、数据与因子构建 2.1 数据 我们的主要数据来源为Global Financial Data,同时利用Bloomberg和DataStream进行了补充。其中大部分数据从20世纪20年代(1920s)开始,少部分可以追溯至1877年2月。同时我们的数据涵盖了股票指数、国债、货币和大宗商品等资产类别。我们还从CRSP提取了近一个世纪美国个股的收益数据与21个国际市场从1984年开始的收益数据。Asness、Moskowitz和Pedersen(2013)曾进行过类似的研究,他们测试了1972年至2010间,价值和动量因子在18种股指期货、10种固定收益证券、10种货币和27种大宗商品上的表现。但我们的样本相较来说更丰富,能够展示更多的信息。 2.2 因子 2.2.1 价值(value) 本文采用了文献中使用的较为简单的定义来构建价值因子,具体的: 1)对于个股(美国个股与国际个股),借鉴Fama and French (1992, 2012) and Asness, Moskowitz, and Pedersen (2013)等人的研究采用了账面市值比率(book-to-market ratio); 2)对于全球股票指数,采用十年期循环调整市盈率—CAPE(指数所有成分股的市值加权市盈率); 3)对于全球债券,采用债券10年期实际收益率(名义收益率与预期通胀之间的差值),其中我们使用3年期消费价格通胀率(3-year trailing Consumer Price Inflation)计算预期通胀。 4)对于货币,采用购买力平价(PPP)汇率,数据主要源于Penn World Tables,一部分信息来自OECD数据库和发布的通胀指数 5)对于大宗商品,我们采用5年现货价格变动的负数。这个用法主要是受DeBondt and Thaler (1985) and Fama and French (1996)等人研究的启发,他们发现长期反转因子和价值因子有强相关性。 2.2.2 动量(Momentum) 参考Jegadeesh and Titman (1993)的研究,本文对所有的资产类别采用一样的动量因子定义:过去12个月的累计收益率。其中Asness研究发现微观结构如bid-ask bounce可能导致短期负的自相关,因此我们跳过了最近一个月的收益。 2.2.3 利差(carry) 我们参考Koijen, Moskowitz, Pedersen和Vrugt (2018)等人的研究,将利差因子定义为市场条件不变情况下的预期资产回报率。具体的: 1)对于股票指数,采用期货前月合约的现货折扣的来衡量。由于这个数据在1990年前不可得,因此我们采用超额股息收益率来计算1990年之前的数据。 2)对于货币,采用两国短期利率差值来计算。 3)对于国债,采用10年期息差(10年期收益率减去3个月利率)。 4)对于大宗商品,采用持有期货合约的回报来计算。如果期货曲线没有变化,我们通过最近和下一个最快到期合约之间的价格变化百分比来衡量。 2.2.4防御(defensive) 防御因子是一个已经被深入研究的因子,通常被用于寻找长期低波动率或低beta的证券。在这里,我们采用了一个简单的防御因子定义,即资产相对于本地市场指数的beta值。具体的, 1)对于股票指数和国债,我们基于本地的股票指数、债券指数进行36个月滚动回归来估算beta。 2)对于货币,我们没有构建防御因子。这是因为目前没有符合逻辑的指数。 3)同样的,我们没有对大宗商品构建防御因子,这主要是由于不同种类的大宗商品彼此的回报并不相关,不能采用统一的指数进行度量。 2.2.5 因子组合构建 针对每类资产,我们利用四类因子构建多空投资组合。其中因子采用上述定义,不考虑交易费用。特别地,对于防御因子,我们构建了有交易成本的投资组合,主要考虑到高beta的组合,往往会有更高的换手率。 首先我们在每个时间截面分别根据四类因子大小对每类资产中的证券进行排序,并根据每个证券的在资产类别中排名分配权重,这里总权重为0。具体地,一只证券在时间t的权重为:

三、因子溢价的存在和大小图表1展示了不同资产类别的收益指标。前四列分别是每个资产类别中四类因子收益率的平均值,标准差,夏普比率和平均收益的t统计量。 前四行是所有资产类别汇总的结果。四类因子夏普比率分别为0.62,0.67,0.84和0.78。同时平均收益的t统计量均超过6,即我们可以认为这些因子的溢价显著不为0。第五行展示的是多因子投资组合的结果,夏普比率提升至1.59,平均收益t值为14.72,这表明通过结合四类因子可以带来多样化的效益。这个结果和Asness,Moskowitz和Pedersen(2013)与Asness,Ilmanen,Israel和Moskowitz(2014)一致,但我们采用的样本期更长,且资产类别更多。
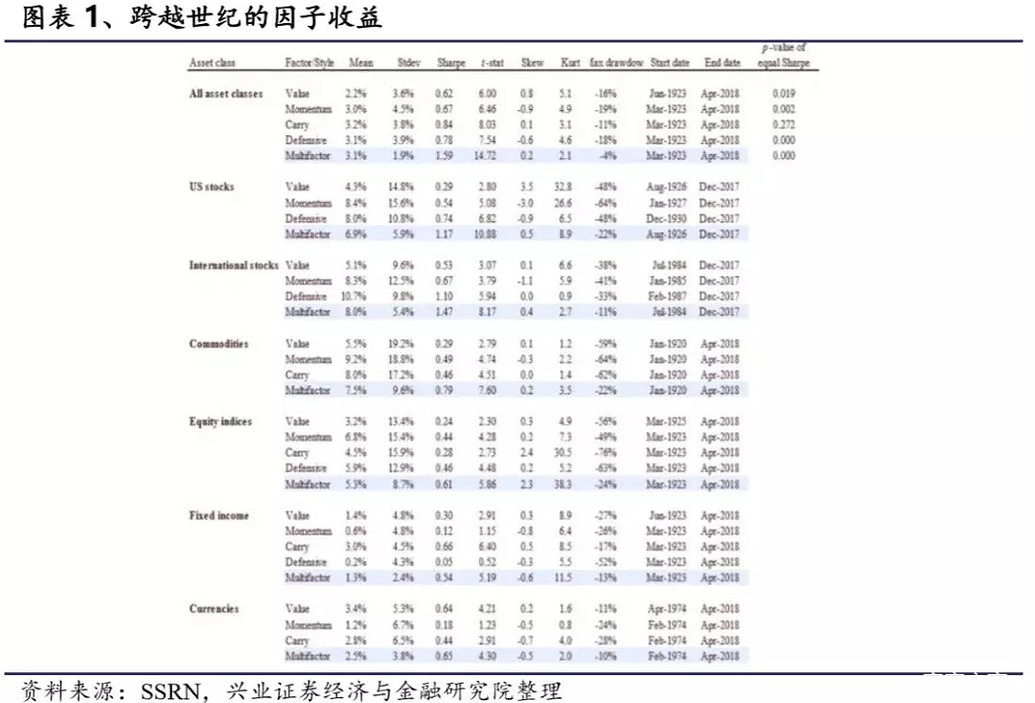
高达14.7的t统计量在一定程度上降低了数据挖掘的可能性。但我们发现本文样本中的很多数据在之前的研究中未曾被使用过,这也让我们产生这些因子的高溢价是否源于数据挖掘的担忧。下面对我们的溢价的可靠性进行说明。 3.1 测试方法 本文使用近半个世纪的样本测试数据挖掘和套利活动对于因子溢价的影响,选用的方法借鉴了Mclean和Pontiff(2016)等人的研究,但我们采用了更长时间的样本和五个额外的资产类别,为研究数据挖掘和知情交易(套利行为)等因素提供了新的视角。 Mclean和Pontiff(2016)测试了1963年至2014年美国市场上众多因子的表现,同时他们将每个因子的样本周期划分为样本内、样本外和因子公开后三个子样本。在他们测试的97个因子中,样本外的收益下降了26%,因子公开后的收益下降了58%。鉴于样本外和发布后两个子样本有部分时间重叠,他们最终将26%的收益下降归结于过拟合,32%的收益下降归结于套利行为。 我们在上述测试的基础上加入了两个新的视角。 首先,由于样本数据时间足够长,我们可以研究在因子被发现之前的效果,我们将这个样本区间被称为“预样本(pre-sample)”。预样本中的测试在研究数据挖掘和套利行为的影响方面特别有效。例如在预样本期间,投资者很少知道因子的作用,可以认为几乎没有套利行为的发生。 其次,我们将样本内和样本外的两个时间段的测试结果对比作为数据挖掘和套利行为的衡量标准。 综上我们可以利用三个样本期的测试结果对数据挖掘和套利行为进行分析。与Mclean和Pontiff(2016)所用的样本后和因子公开后相比,我们所采用的预样本数据可以加入更多的信息。但需要注意的一个问题是,预样本的数据质量可能较差,从而对结果造成一定的影响。下面是对不同因子进行检验的结果。 3.2 价值因子测试结果 对于价值因子,我们使用Fama和French(1992)的样本期,1963年7月到1990年7月,作为原始样本期。同时出于以下两个原因,我们对股票之外的资产类别也采用一样的时间段: 1)其他资产类别的研究往往比较新,这会造成样本后的时间较少。 2)我们认为:一旦一个因子在一个资产类别中发现是有效的,它可以被立刻用于其他市场。当然这个假设与事实不完全相符。 图表2展示了美国股票三个样本期的夏普比率,可以看出价值因子在原始样本期的表现优于预样本和样本后两个时间段的,意味着可能存在过拟合偏差。同时我们注意到三个样本期的夏普比率均为正数,说明价值因子的溢价并非全部源于数据挖掘。价值因子预样本时期比样本后的表现更好,这意味着价值因子的作用可能由于套利行为有所下降。然而,其他资产类别的结果大为不同。 对于国际股票,样本后的夏普比率几乎是原始样本期的两倍。但由于1984年才有国际股票数据,因此我们未能进行预样本测试。 对于大宗商品、股票指数、国债而言,原始样本期的表现优于预样本和样本后时期,但样本后的表现优于预样本。 我们在所有资产类别中测试原始样本期和样本外时期的夏普比率是否相等,p值仅为0.048,因此统计上我们认为样本期和样本外的夏普比率是不相等的。同时我们测试预样本和样本后时期的夏普比率是否相当,p值为0.924,即统计上预样本和样本后不存在差异。

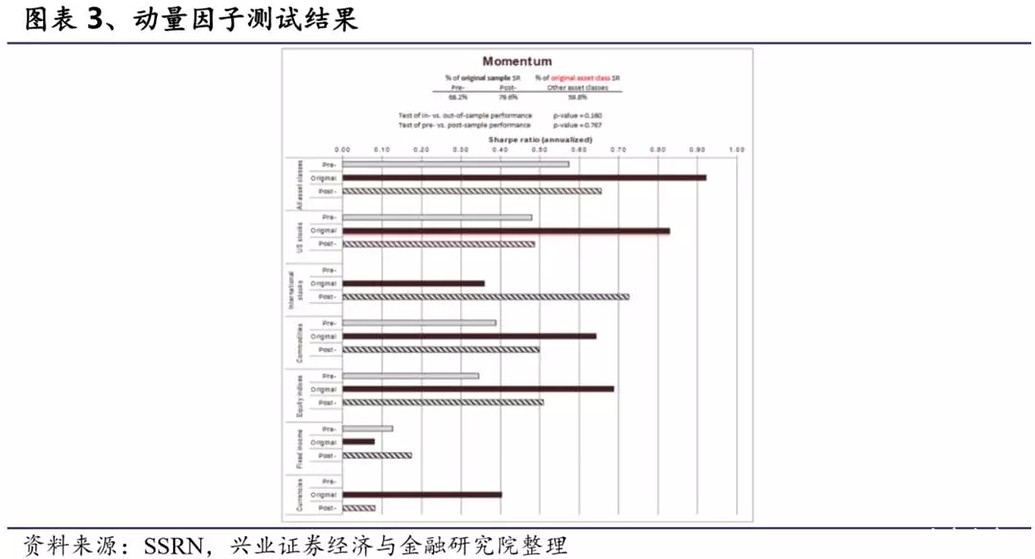
综合所有资产类别,价值因子在原始样本的夏普比率为1.0,样本后时期为0.75,预样本时期为0.30。预样本的平均夏普比率为原始样本的36%,样本后的结果为原始样本的78%。与我们之前在美国股票中得到的结论一致,即原始样本中存在过拟合但并非所有的因子溢价都源于过拟合。同时我们结论并不支持套利行为会影响因子溢价结果。我们还发现价值因子在其他资产类别中的表现比在美国股票中的表现高约24%,这表明价值因子并非仅适用于美国股票市场,在其他资产类别中也存在着一定溢价。 3.3 动量因子测试结果 我们使用Jegadeesh和Titman(1993)的样本期作为原始样本期,即1964年1月到1989年12月。由图表3,可以看出样本外的动量因子溢价依旧显著,即动量因子的溢价并非是虚假的。但同样的我们发现样本外的表现逊于原始样本的。这也说明动量因子溢价有一部分源于过拟合,但并非全部源于数据挖掘。同时,值得注意的是,对于动量因子我们没有拒绝样本内外表现相同的原假设(p=0.160)。我们也没有发现样本后的动量比预样本时期表现差的一些证据,这说明套利行为对动量因子的影响不大。 上述结论适用于我们测试的所有资产类别,同时动量因子在其他资产类别中的夏普比率大约是美国股票中的60%。
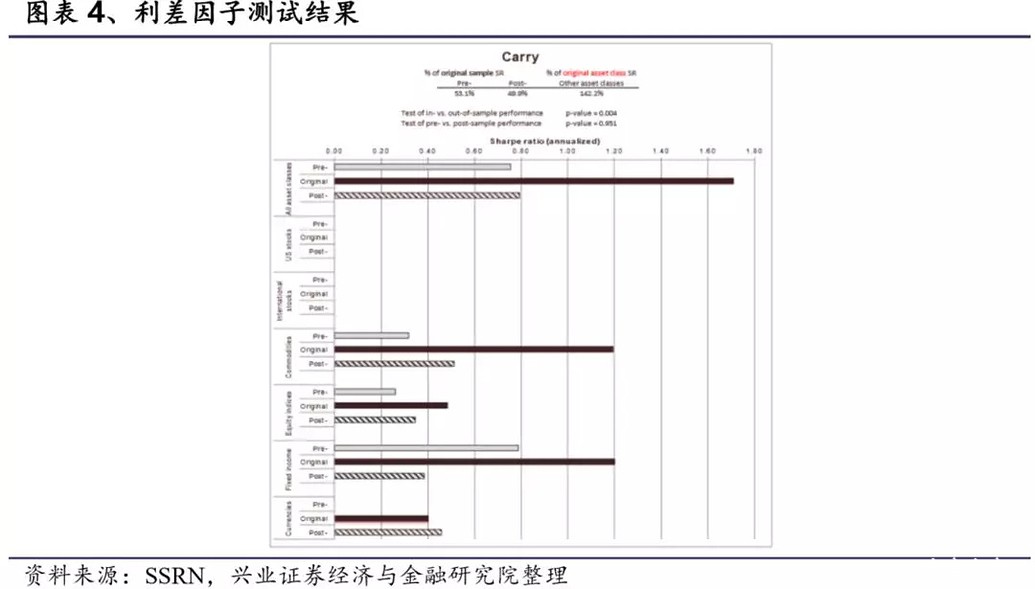
3.4 利差因子测试结果 利差因子源于Meese,Rogoff(1983)和Fama(1984)等人的研究,他们发现了货币的“远期溢价之谜”( forward premium puzzle)。其中Meese and Rogoff(1983)采用的样本期为1973年3月至1981年6月,Fama(1984)采用的样本期为1973年8月至1982年12月。结合两者,我们使用1973年到1982年作为原始样本。这也意味着,对于货币我们未能构建预样本时期,因为在1973年1月之前,汇率是根据布雷顿森林体系(Bretton Woods)构建的。 由图表4可以看出货币的样本外夏普比率大于样本内,这表明因子溢价未受数据挖掘影响。同时套利行为也不会影响因子样本外表现。在其他类别中,利差因子预样本和样本后的效果约为原始样本的一半,表明存在过拟合。同时我们样本内与样本外表现一致的原假设没有被拒绝(p=0.951),这说明因子溢价不会因为套利行为而减弱。同时在利差因子在货币以外资产类别中的表现要比货币高出42.2%,这表明利差因子并非仅适用于货币。
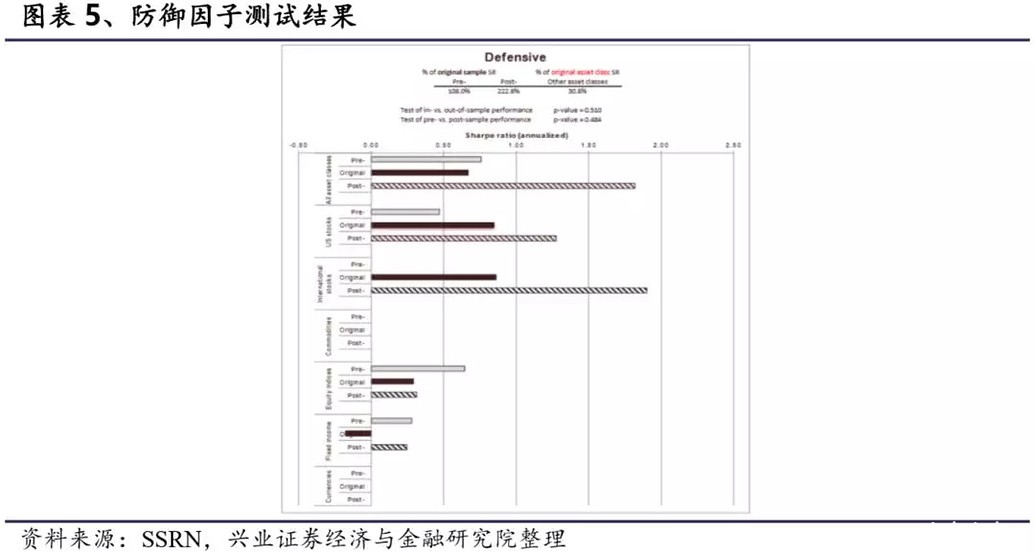
3.5 防御因子测试结果 前文我们提到防御因子在学术上已被深入研究。Black(1972,1992)进行了风险厌恶对CAPM影响的实证检验。Ang等人(2006,2009)表明低波动性可以预测股票回报。然而,Frazzini和Pedersen(2013)建立了我们在本研究中使用的betting-against-beta (BAB)因子,涵盖了最长的样本周期。因此,本文将原始样本周期设为1960年至2009年。 具体的,防御因子在预样本和样本后的表现都优于原始样本,这排除了因子溢价是源于过拟合。此外,样本后表现优于预样本说明防御因子的表现不会因为套利行为而降低。我们对样本内、外表现进行检验未发现显著差异。对比防御因子在美国个股中与其他资产的表现,可以看出防御因子在美国个股中表现最好。
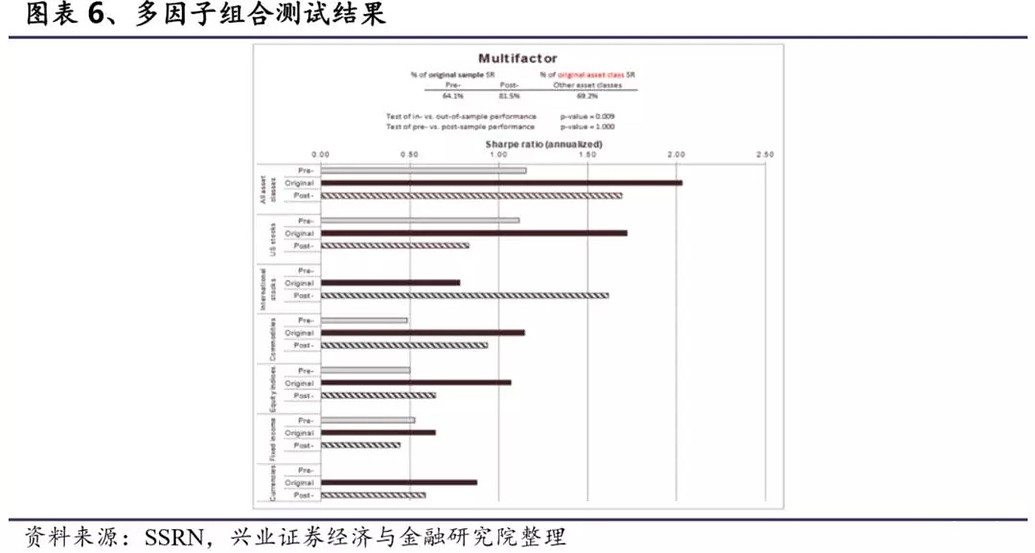
3.6 多因子组合测试结果 对于多因子投资组合,定义原始周期较为复杂。为了我们的原始周期适用于四类因子,我们可以取前面四个原始周期的并集,即1960年到2009年,或他们的交集,即1973年到1981年。这两种方式都有其优缺点,综合考虑我们将原始样本期定义为1960年至1990年,涵盖了所有因子的大部分样本内期。 多因子组合的测试结果与我们之前的研究结果相呼应,预样本的夏普比率约为原始样本夏普比率的64%,样本后夏普比率约为原始样本夏普比率的69%。同时通过统计检验,我们证明了样本外性能会降低(p=0.009),但是预样本和样本后的收益差异不显著(p=1)。 总的来说,我们发现因子溢价是存在的,并且在样本外也稳健。然而因子溢价的样本外表现会由于过拟合下降约30%,这和Mclean and Pontiff (2016)得到的结果类似。但与Mclean和Pontiff(2016)的结果不一致的是,我们发现因子在公开后受套利行为的影响是很小的。
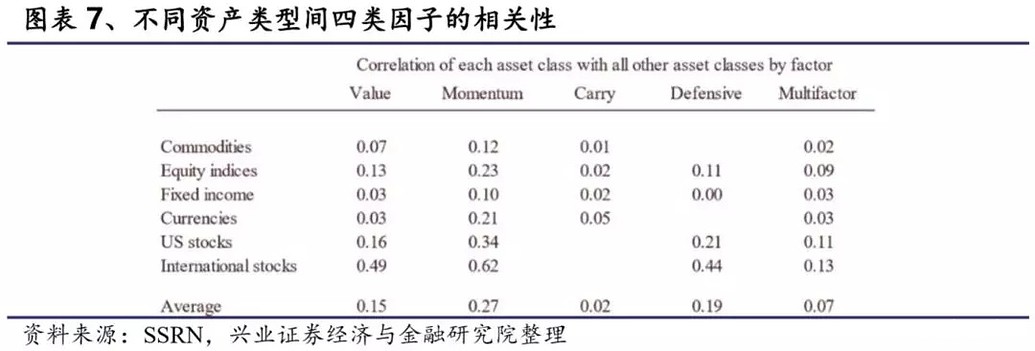
四、因子溢价来源在上文对因子溢价的可靠性进行检验之后,我们基于风险和行为理论对因子溢价进行解释。 4.1 共同变化-因子间的相关性 首先我们测试同一因子不同资产间与同一资产不同因子间的相关性,以此得到因子的共同驱动部分。 图表7展示了同一因子在不同资产间的相关性(月度收益的相关性)。第一列是每个资产类别的价值策略与其他资产类别价值因子的相关性,平均值为0.15。之后的列含义相同,但分别是动量因子、利差因子、防御因子和多因子组合的结果。我们得到的结果符号和大小与Asness,Moskowitz和Pedersen(2013)的结果一致,但我们增加了50年的样本。同时对于利差策略,与Koijen,Moskowitz,Pedersen和Vrugt(2018)研究结果一致,不同资产之间的相关性极小。同时。我们得到的关于防御策略的结论是其他文献中未曾研究的。
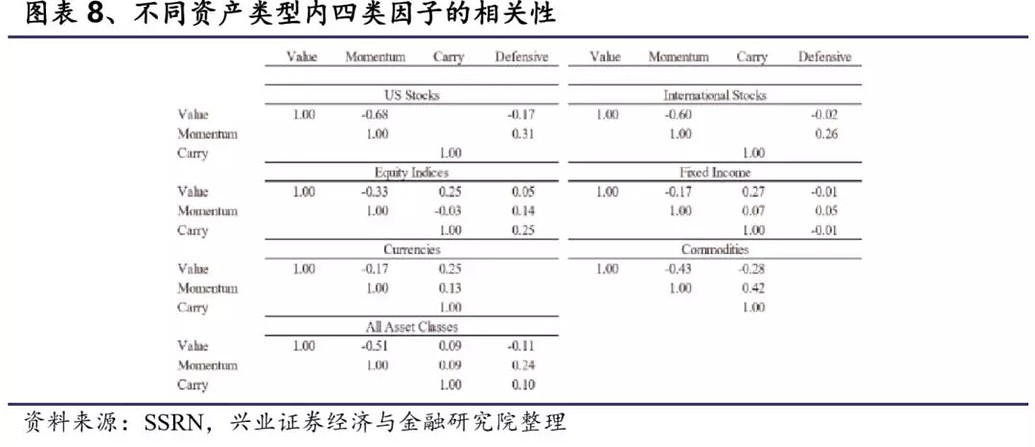
图表8展示了每个资产类别中各因子的相关性。在美国个股中,价值因子和动量因子呈现负相关(-0.68),价值因子和防御因子有微弱的负相关关系(-0.17),同时动量和防御因子呈正相关(0.31)。国际股票的结果和美国个股类似。同时对于非股票类型的资产,价值和动量之间存在一致的负相关关系(平均-0.51)。 每个资产中动量和防御因子始终呈正相关。价值和防御在每个资产类别中始终呈负相关,但是相关性很小。利差因子和价值因子在股票指数、债券、货币中呈现正相关,但在商品中呈现负相关。同时除了商品中利差因子和动量因子正相关(0.42),在其他资产类别中利差因子和动量因子都不相关。
由图表9可得: 1)每类资产中的每类因子对同一资产中其他三类因子回归的结果; 2)每类资产中的每类因子对其他资产中的相同因子进行回归的结果。 同时在回归中加入了股票、债券和大宗商品市场指数。我们发现各因子对其他资产类别中同一因子进行回归的系数均显著为正,说明因子在所有资产中存在共同变化。然而,在控制同一资产类别中的其他因子,其他资产类别中的相同因子以及股票,债券和商品的市场投资组合之后,我们发现每个资产类别几乎每个因子都具有显著的正alpha,表明此共同变化仅捕获每个资产类别中每个因子溢价的一部分。

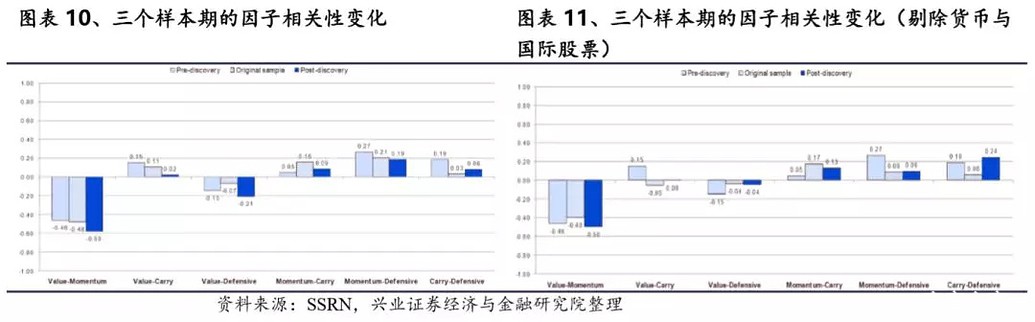
4.2 套利行为 通过上述研究我们发现套利活动并没有对这些因子的表现产生很大的影响,下面我们主要研究套利活动是否会影响因子间的相关性,即在预样本、原始样本与样本后三个样本期中因子的相关性是否一致。 通过上述检验我们可以从另外一个视角来研究是否存在过拟合。Linnainmaa和Roberts(2016)认为数据挖掘偏差会人为的降低样本中因子的相关性,这是因为过拟合可能会通过最小化与其他因子的相关性来获得高信息比。纯粹由数据挖掘得到的因子只是噪声,在样本内外与其他资产类别不会表现出太大的相关性,尤其是在一个资产中过拟合。 接下来,我们在预样本、原始样本、样本后三个时间段上计算了单一因子在不同资产间的相关性和单一资产中不同因子的相关性。如果在样本外的相关性更高且同一因子在不同资产间的相关性较弱,我们认为因子可能存在过拟合的风险。同时源于数据挖掘的因子应该在预样本期的相关性更低。 图表10展示了同一资产中不同因子的在三个时间段相关性平均值的变化,可以看出在样本后相关性并没有显著的提升反而略有下降。由于货币和国际股票时间周期短,可能会限制我们的分析,在图表11中我们剔除这两类资产进行了计算。同样的,没有证据表明样本外各因子之间的相关性更高。
图表12测试了单一因子在不同资产中的相关性均值。第一个柱子是价值因子在不同资产中的相关性均值。不同资产类别价值因子的平均相关性在预样本期间最低,在原始样本期较高,样本后最高。动量因子也表现出同样的模式,但利差因子或防御因子并没有同样的模式。这些结果表明,随着时间的推移,价值和动量在不同市场之间的相关性可能变得更强,这可能是随着对因子认知程度的加深,投资者积极进行交易;或是市场一体化的程度加高。然而这个结论可能不那么可靠,因为国际股票和货币没有预样本的数据,而美国股票和国际股票高度相关。我们在图表13中展示了剔除货币和国际股票之后,价值因子、利差因子和防御因子的相关性,可以看出都不再显著。动量因子在样本后相关性略有提升,但差距不明显。这说明套利行为并没能对因子相关性产生较大的影响。
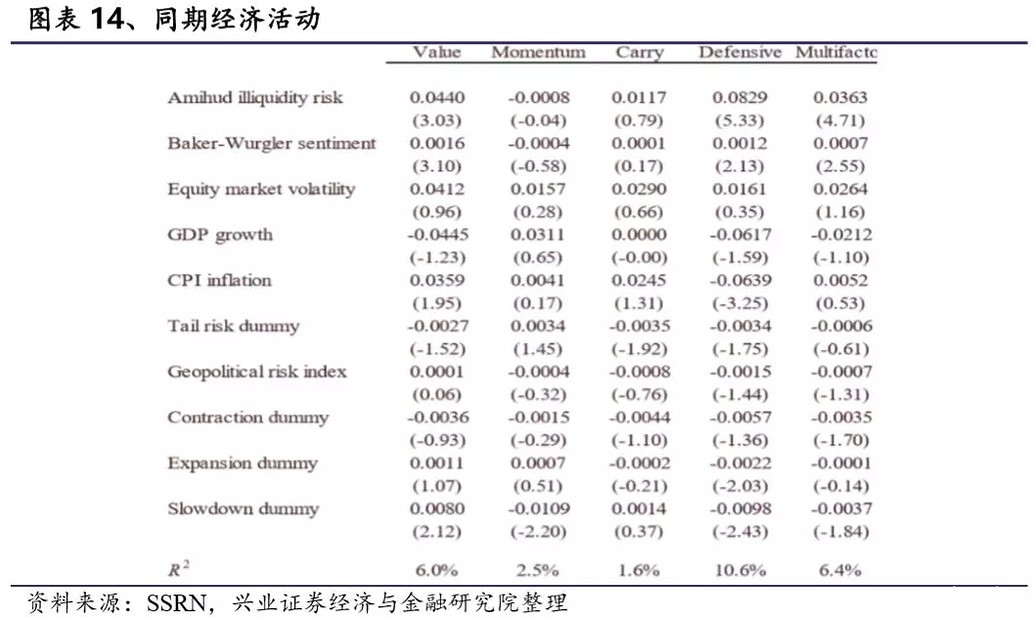
4.3 经济风险 许多资产定价理论试图通过系统性风险或经济中不断变化的投资机会状态变量来度量因子的共同变化。我们收集一系列与经济活动有关的变量,测试因子收益和这些变量之间的相关性,从而来检验描述因子溢价来源的若干理论。由于样本有限,将因子表现和经济风险联系起来具有较大难度。我们使用时间跨度更长、资产类型更广泛的样本集来测试不同市场经济事件与因子溢价之间的关系。同时由于我们的样本中包含的资产类别更丰富,可以减少一些结果的噪声。 4.3.1 经济活动变量与因子溢价关系 在本节中我们测试了下列变量与因子溢价的关系,具体变量构建方法如下所示: - Amihud (2014)提出的度量流动性风险的指标—Amihud illiquidity risk,此指标有利于度量套利行为对因子溢价造成的影响大小。
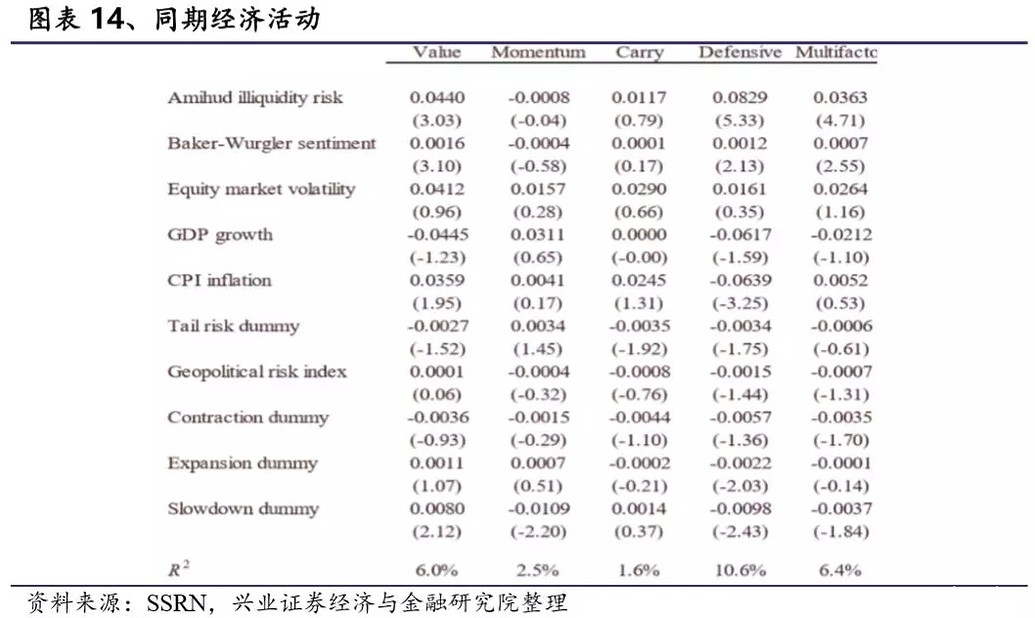
2)Baker和Wurgler(2008)提出的Baker and Wurgler (2008)情绪指标,此指标旨在捕捉投资者的情绪。Baker和Wurgler认为投资者的情绪与因子溢价有很大联系。 3)股票市场波动指标—Equity Market Volatility,此指标以过去36个月的平均加权国家指数的实际波动率计算。市场波动可以度量一部分套利成本,同时代表了市场中的风险和不确定性,这也会对因子溢价造成影响。 接下来的变量主要与宏观经济活动有关,试图将因子溢价与宏观经济模型联系起来。这里存在的一个问题是相关研究资料较少,例如因子与宏观经济如何相互作用?宏观经济会如何影响因子?我们能够从直观逻辑出发得到经济增速或通胀会对股票或债券市场会产生什么样的影响。然而价值因子、动量因子、利差因子、防御因子会受到怎样的影响呢?同时由于这四类因子彼此之间低相关甚至可能是负相关的,它们面对的风险可能是完全不同的。在没有完整理论指导的情况下,我们对宏观经济活动与因子之间的关系进行探究,但我们必须承认在这种无完整理论指导的研究可能会带来一定的数据挖掘风险。图表14、15中我们还采用了: 4)全球GDP增长:超过去年美国、德国、日本、英国平均值的GDP; 5)CPI通胀:超过去年美国、德国、日本、英国平均值的通胀率; 6)尾部风险的虚拟变量:如果该国家为尾部5%则记为1,反之则记为0; 8)三个商业周期指标。具体地,我们利用每季度GDP同比增长和每季度GDP同比增长的变化两个指标来构建经济的四个状态: 收缩:GDP同比增长和每季度GDP同比增长变化都为负数; 复苏:GDP同比增长为负数而每季度GDP同比增长变化为正数; 扩张:GDP同比增长和每季度GDP同比增长变化都为正数; 放缓:GDP同比增长为正数而每季度GDP同比增长变化为负数; 同时为了避免频繁的状态切换,我们设置四个状态的切换需要GDP同比增长和每季度GDP同比增长变化达到一定阈值。即GDP同比增长或每季度GDP同比增长变化的值超过过去10年的1倍标准差时,才进行切换 宏观经济变量的一个重要问题是它们的公布时间。许多经济变量例如GDP等公布的都较晚,可能会延迟一个季度才对外公告。这就衍生出两种处理方式。第一种方式是:将宏观变量进行同期匹配。例如将第二季度的股票收益与第二季度的GDP数据相匹配。这是考虑到GDP是在第二季度产生的,是当时实际的GDP。第二种方法是:将GDP数据与GDP对外发布后的股票收益匹配起来。这主要考虑到在对外发布之前市场并不能了解GDP数据。我们在图表14、15中分别测试了这两种方法的结果。 图表14的第一列展示了价值因子的测试结果。可以看出价值因子收益与流动性风险, 情绪指标和经济放缓指标有显著的正相关关系。即当流动性风险更高、情绪高涨或经济放缓时价值因子收益会更高。前两种效应分别与Asness,Moskowitz和Pedersen(2013)以及Baker和Wurgler(2008)的研究一致。其余变量对价值回报没有显著影响。 动量仅和经济放缓变量有显著的负相关关系,与其他变量的相关性都不显著。动量因子的系数符号大多和价值因子的结果相反,这可能源于动量因子与价值因子的负相关关系。 类似的,利差因子与任何变量都不存在显著的相关关系,其中最显著的是尾部风险虚拟变量(t=-1.92),这和Brunnermeier,Nagel和Pedersen(2009)的研究结果一致。 同时我们发现当非流动性风险较高和情绪高涨时,防御因子的收益更高。但在通胀较高以及在经济扩张或经济放缓期间防御因子会有较低的回报。 总体而言,没有太多证据表明这些因子与经济变量有显著相关关系。模型的R2都很小,系数大多不显著同时符号也不稳定。即使使用更长的样本也未改变这个结果。如果采用 Bonferroni调整的t统计量,没有一个宏观变量和因子收益显著相关。
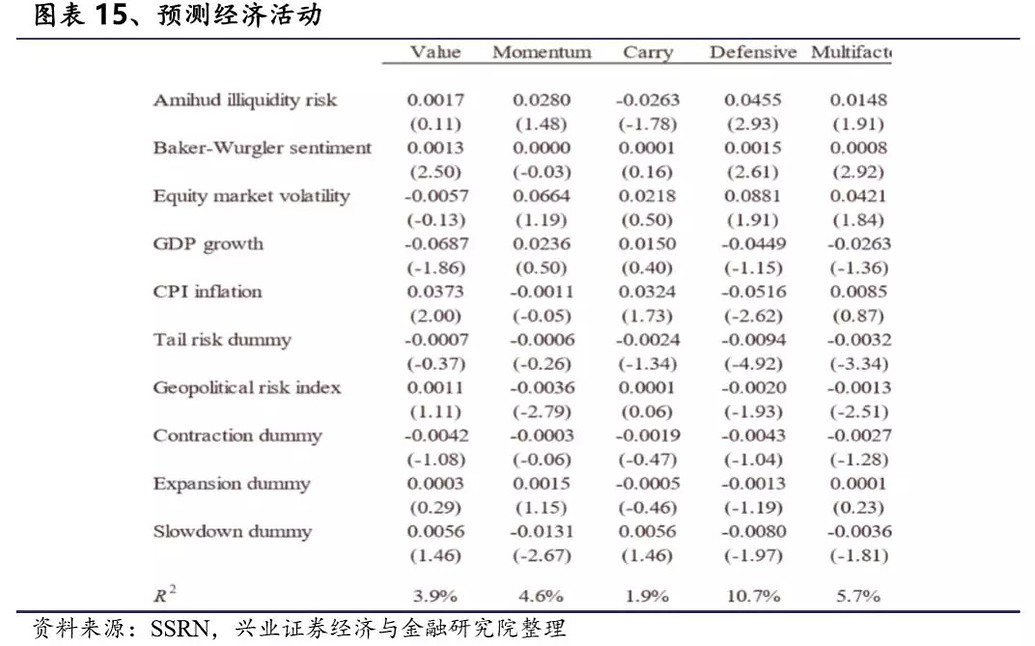
图表15展示了第二种方法测试出的结果。由于这些经济变量时间是滞后的,我们也认为这是在对经济活动做预测。可以看出模型的R2都很小,同样的,如果采用Bonferroni调整的t统计量,没有一个宏观变量和因子收益显著相关。
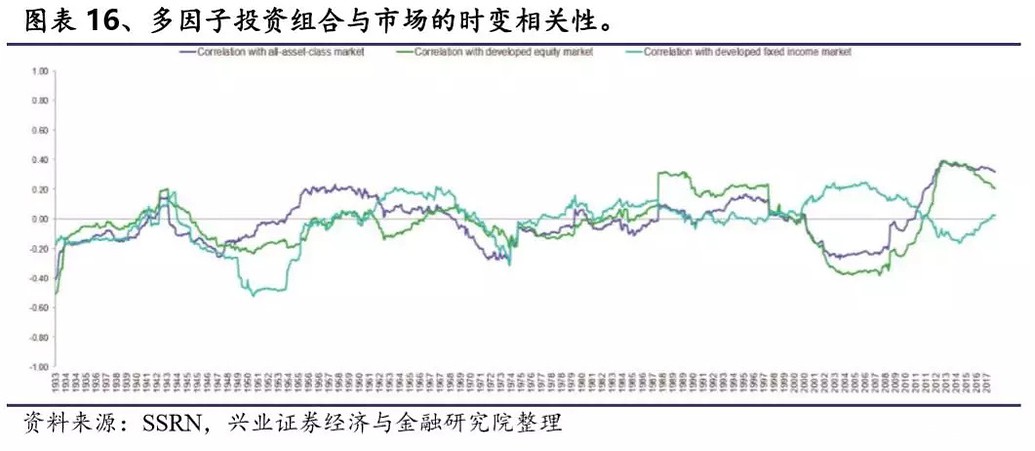
接下来我们采用全球市场投资组合的收益来构建经济活动代理变量,这里采用三种市场代理变量:全资产类市场投资组合,全球股票市场投资组合和全球固定收益投资组合。我们计算多因子组合和市场代理变量收益的时变相关性。如图表16所示,这些市场代理变量中的每一个的平均相关性都接近于零,且不能拒绝相关性为零的原假设。
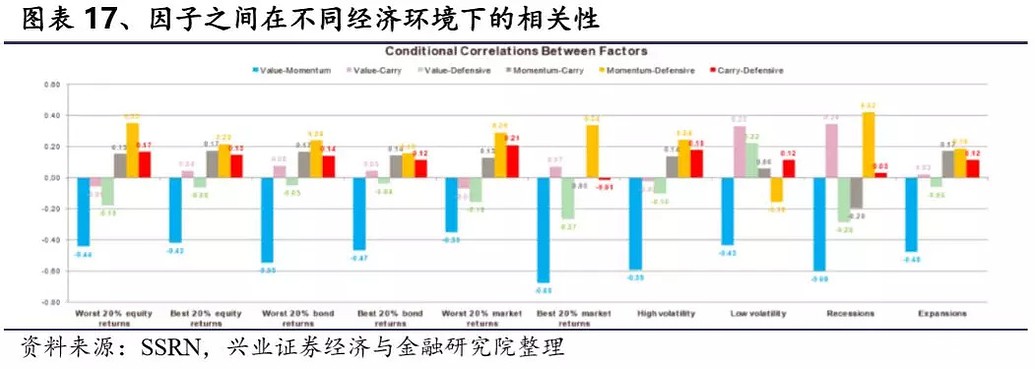
尽管我们使用了更为丰富的样本,但并没能发现四类因子收益与经济活动有显著相关性。这个结果和Griffin,Ji和Martin(2003),Asness,Moskowitz和Pedersen(2013)得出的结论基本一致。但与(Chordia和Shivakumar(2005),Hodges,Hogan,Peterson和Ang(2017))不一致,这可能是由于他们都采用的样本期更短。 4.3.2不同经济环境中的相关性 我们还研究了不同经济环境对于因子之间的相关性是否会有所影响。首先我们划分不同的经济环境: 1)全球股票月收益(MSCI指数)最好和最差的20%的月份 2)全球债券月收益率(巴克莱银行综合债券指数)最好和最差的20%的月份 3)包括股票,债券和商品在内的所有资产类别的波动率加权平均值的收益率最好和最差20%的月份 4)股票市场波动率(过去36个月的实际波动率)的最高和最低20% 5)使用NBER的商业周期定义应用全球经济衰退和扩张期间 图表17展示了单一资产内不同因子间相关性的平均值。可以看出在不同经济环境下相关性并没有很大变化,特别在极端的负面事件中也没有发现因子之间的相关性上升。
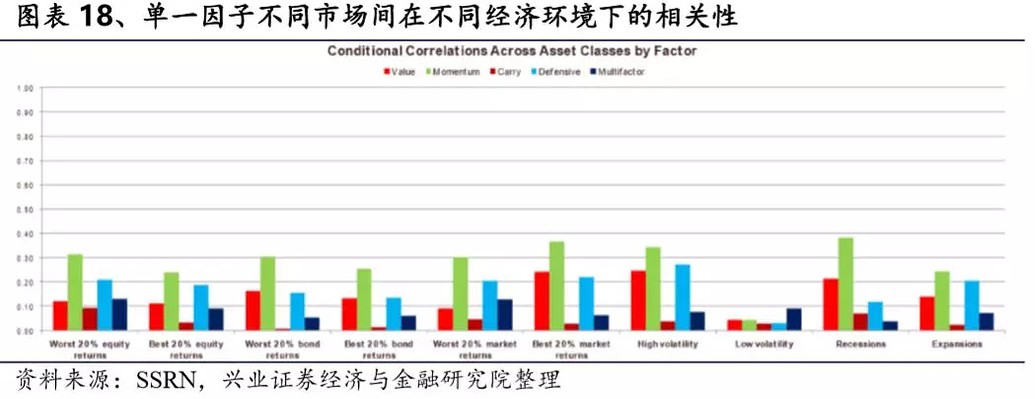
图表18展示了单一因子在不同资产类型间相关性的平均值。我们未能发现不同资产间的相关性会随市场状态发生变化的证据。当然其中有一个例外,当市场波动率非常低(最低20%)时,一些因子的相关性会特别低。我们认为在此时多样化的效益最大,从投资的角度来看有效的投资组合能够在市场最动荡的时期获得最大的收益。
参考文献 【1】Bernardo, J. M., and A. F. M. Smith. Bayesian Theory. Hoboken: Wiley, 1994. Adrian, T., R. K. Crump, and E. Moench (2015), “Regression-based estimation of dynamic asset pricing models,” Journal of Financial Economics 118 (2), 211–244. 【2】Akbas, F., W. J. Armstrong, S. Sorescu, and A. Subrahmanyam (2015). Smart money, dumb money, and capital market anomalies. Journal of Financial Economics 118 (2), 355–382. 【3】Arnott, R. D., N. Beck, and V. Kalesnik (2016a). Timing “smart beta" strategies? Of course! Buy low, sell high! Working paper, Research Affiliates. 【4】Arnott, R. D., N. Beck, and V. Kalesnik (2016b). To win with “smart beta" ask if the price is right. Working paper, Research Affiliates. 【5】Arnott, R. D., M. Clements, V. Kalesnik, and J. Linnainmaa, (2018), Factor momentum. Working paper, Research Affiliates. 【6】Asness, Clifford, Tobias J. Moskowitz, and Lasse Pedersen (2013), “Value and Momentum Everywhere,” Journal of Finance 68 (3), 929-985. 【7】Asness, Clifford, Andrea Frazzini, and Lasse Pedersen (2016), “Quality Minus Junk,” AQR Capital Working paper. 【8】Asness, C., A. Ilmanen, and T. Maloney (2017), Market timing: Sin a little, Journal of Investment Management, 15 (3), 23-40. 【9】Asness, C., S. Chandra, A. Ilmanen, and R. Israel (2017). Contrarian factor timing is deceptively difficult. The Journal of Portfolio Management 43 (5), 72–87. 【10】Asness, C. S. (2016). The siren song of factor timing aka “smart beta timing" aka “style timing". The Journal of Portfolio Management 42 (5), 1–6. 【11】 Asness, C. S., J. A. Friedman, R. J. Krail, and J. M. Liew (2000). Style timing: Value versus growth. Journal of Portfolio Management 26 (3), 50–60. 【12】Baker, M. and J. Wurgler (2006). Investor sentiment and the cross-section of stock returns. The Journal of Finance 61 (4), 1645–1680. 【13】Bakshi, G. and G. Panayotov (2013). Predictability of currency carry trades and asset pricing implications. Journal of Financial Economics 110 (1), 139–163. 【14】Baltussen, G., L. Swinkels, and P. Van Vliet (2019), Global factors premiums. Robeco Working Paper. Barberis, N., R. Greenwood, L. Jin, and A. Shleifer (2015). X-CAPM: An extrapolative capital asset pricing model. Journal of Financial Economics 115 (1), 1–24. 【15】Belo, F., ‘Production-based measures of risk for asset pricing’, Journal of Monetary Economics, Vol. 57, 2010, pp. 146–163. 【16】Brooks, Jordan and Tobias J. Moskowitz (2017), “Yield Curve Premia,” AQR Capital and Yale University Working paper. 【17】Campbell, J. and R. Shiller (1988). The dividend-price ratio and expectations of future dividends and discount factors. Review of Financial Studies 1 (3), 195–228. 【18】Cohen, R. B., C. Polk, and T. Vuolteenaho (2003). The value spread. The Journal of Finance 58 (2), 609–641. 【19】Cooper, I. and R. Priestley (2008). Time-varying risk premiums and the output gap. The Review of Financial Studies 22 (7), 2801–2833. 【20】Cooper, I. and Priestley, R., ‘Real investment and risk dynamics’, Journal of Financial Economics, Vol. 101, 2011, pp. 182–205. 【21】Daniel, Kent and Tobias J. Moskowitz (2016), “Momentum Crashes,” Journal of Financial Economics 122 (2), 221-247. Ehsani, S. and J.T. Linnainmaa (2019), “Factor Momentum and the Momentum Factor.” Working paper. 【22】Estrella, A. and F. S. Mishkin (1997). The predictive power of the term structure of interest rates in europe and the united states: Implications for the european central bank. European economic review 41 (7), 1375–1401. 【23】Fama, E. and R. Bliss (1987). The information in long-maturity forward rates. The American Economic Review, 680–692. 【24】Fama, E. and K. French (1988). Dividend yields and expected stock returns. Journal of Financial Economics 22 (1), 3–25. 【25】Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stock and bonds. Journal of Financial Economics 33, 3–56. 【26】Fama, Eugene F. and Kenneth R. French (1996), Multifactor explanations of asset pricing anomalies. Journal of Finance 51, 55–84. 【27】Fama, Eugene F. and Kenneth R. French (2012), Size, value, and momentum in international stock returns. Journal of Financial Economics. 【28】Frazzini, Andrea, and Lasse H. Pedersen (2013), “Betting against beta,” Journal of Financial Economics 111 (1) 1-25. 风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成, 在政策、市场环境发生变化时模型存在失效的风险。 作者:兴业证券金工团队
|