|
多因子选股模型在模型搭建中,往往会涉及到非常多的股价影响因子,并可能导出数量极多的备选模型。因此,对于多因子选股模型的评价和筛选,就显得尤为关键。对于专业的量化投资人而言,就需要进一步了解多因子选股模型的两种主要的评价判断方法——打分法和回归法。
1、打分法的评价原理和流程 所谓打分法,就是根据各个因子的大小对股票进行打分,然后按照一定的权重加权得到一个总分,最后根据总分再对股票进行筛选。对于多因子模型的评价而言,实际通过评分法回测出的股票组合收益率,就能够对备选的选股模型做出优劣评价。 打分法的优点是相对比较稳健,不容易受到极端值的影响。但是打分法需要对各个因子的权重做一个相对比较主观的设定,这也是打分法在实际模型评价过程中,比较困难和需要模型求取的关键点所在。 进一步从打分法的流程来看,多因子选股模型的建立、评价和改进流程,大致可以分为4个步骤: 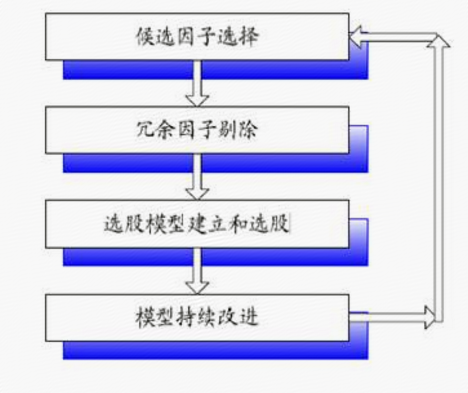
此外,对于量化选股打分法,专业人士还提示指出,一方面,多因子选股模型中有的因子会逐渐失效,而另一些新的因子可能被验证有效而加入到模型当中;另一方面,一些因子可能在过去的市场环境下比较有效,而随着市场风格的改变,这些因子可能短期内失效。在这种情况下,对综合评分选股模型的使用过程中,需要对选用的因子、模型本身做持续的再评价和不断的改进以适应变化的市场环境。除此之外,在计算综合评分的过程中,除了各因子得分的权重设计之外,交易成本和风险控制等因素,也同样需要予以综合考量。
2、多元线性回归简介 所谓回归法,就是用过去的股票的收益率对多因子进行回归,得到一个回归方程,然后再把最新的因子值代入回归方程得到一个对未来股票收益的预判,然后再以此为依据进行选股,并对选股模型的有效性和收益率进行评价。 回归法的优点是能够比较及时地调整股票对各因子的敏感性,而且不同的股票对不同的因子的敏感性也可以不同。回归法的缺点,则是容易受到极端值的影响,在股票对因子敏感度变化较大的市场情况下效果也比较差。 在线性回归分析中,如果有两个或两个以上的自变量,就称为多元线性回归。因此,通过多元线性回归对多因子选股模型进行评价,也能够得到一个直观的股票组合收益率结果,同时能够有效评价该选股模型的优劣。 从数学的角度来说,假设因变量Y(预期收益率)是自变量X1,X2,X3..Xk(候选因子)的线性函数,用方程来表示就是: Yi=β0+β1X1i+β2X2i+...+βkXki+εi 其中,Yi表示因变量(被解释变量)的第i个观测值,而Xki则是第k个自变量(解释变量)的第i个观测值,是自变量Xk的系数,εi是第i组观测值的残差项。在金融领域,β0有时候会写成α,该方程来表示也可以写作: Yi=α+β1X1i+β2X2i+...+βkXki+εi 在此之中,多元线性回归通常采用普通最小二乘法(OLS)进行估计,普通最小二乘估计法的思路是改变β0,β1,β2,...,βk,使得残差的平方和最小。 从回归法的流程来看,多因子选股模型的建立、评价和改进流程,大致可以分为6个步骤: 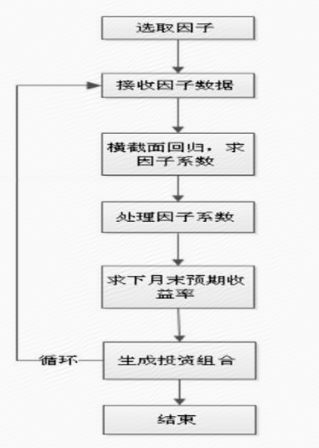
|